MacBidouille

Les interférences lumineuses

  Nous venons donc de voir qu'une onde lumineuse pouvait s'écrire mathématiquement sous la forme complexe suivante :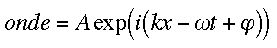

  Mais que se passe-t-il si deux ondes se superposent, en clair si deux ondes arrivent au même moment au même endroit? Si les deux ondes sont des ondes lumineuses, on pourrait croire qu'on va au final en obtenir une qui sera deux fois plus brillante. Et comme par hasard, la réponse est : "c'est faux". Les maths et la physique, ce n'est pas toujours simple :-)
  Comme nous l'avons vu avant avec un exemple constitué d'une bougie et d'un miroir, deux ondes lumineuses peuvent partir en même temps d'une même source, mais ne pas arriver en même temps en un point donné, si les deux ondes n'ont pas suivi le même chemin. Et dans ce cas, ce qui va être intéressant, c'est le déphasage (la différence de phase) entre les deux ondes. Ce qui nous intéresse, c'est précisement le déphasage entre les deux ondes, et non pas à quel moment elles arrivent. Plutôt que de donner une phase à chaque onde et de faire la différence entre les deux phases, on va supposer que la première onde est une onde de référence pour la phase, donc qu'elle a une phase nulle, et que seule la deuxième onde aura une phase. Plus concrétement, si deux personnes font une course et que l'une met 10 secondes et l'autre 11 pour arriver, et que ce qui nous intéresse correspond à l'écart entre les deux coureurs, on peut dire que le premier coureur a mis 0 seconde, et que le second coureur a eu besoin d'une seconde. L'écart reste le même, et c'est tout ce dont on a besoin.
  Soient donc deux ondes, l'une ayant une phase nulle, qui sera donc la référence, et l'autre ayant une phase phi quelconque. Comme on se place en un point donné, la variable d'espace de l'équation de l'onde ne va pas nous intéresser pour le moment. On peut donc simplifier pour les calculs l'équation de nos deux ondes :

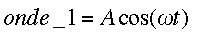
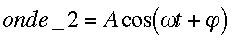
  La variable d'espace x a disparu dans les deux équations, car on se place en un point donné, donc cette variable n'intervient plus en quelque sorte. L'onde 1 a une phase nulle, seule l'onde 2 a une phase non nulle phi comme indiqué ci-dessus. De plus, l'exponentielle complexe s'est transformée en un cosinus. Pour les calculs de ce genre, il est très pratique de passer du monde complexe (imaginaire) au monde réel, puis de repasser si besoin dans le monde complexe. Je ne détaille pas tous ces calculs qui seraient trop compliqués pour bon nombre d'entre vous je pense.
  On peut alors montrer que la superposition des deux ondes va donner un résultat suprenant, qui peut être de ce genre :

  Ce résultat est quand même surprenant dans le sens où nous avons superposé deux ondes lumineuses issues d'un seul Laser rouge, qui au final vont donner soit de la lumière soit du "noir". Dans certains cas, nous avons donc "lumière+lumière=lumière", dans d'autres "lumière+lumière=obscurité". Essayons de voir comment cela est possible.
  Mathématiquement, le résultat de la superposition des deux ondes onde_1 et onde_2 peut se mettre sous cette forme :

  Le résultat est en vrai un tout petit peu plus compliqué, mais il y a là tout ce dont nous avons besoin. La lumière qui résulte de la superposition des deux ondes va avoir une certaine intensité, et va surtout dépendre de la phase comme nous l'avons dit tout à l'heure. Si l'oeil ne peut pas voir la phase d'une onde, il peut par contre voir le résultat qu'elle produit, ce qui est le cas ici. La phase qui va modifier la valeur du cosinus et donc le résultat en fait va créer un phénomène que l'oeil humain peut voir, celui des interférences lumineuses. En fait, la fonction cosinus est une fonction dont le résultat varie entre -1 et +1, suivant la valeur de la phase dans notre cas présent. Si la valeur de la phase phi est telle que le cosinus vaut 1, alors l'intensité vue par votre oeil sera maximale, ce qui correspond aux ronds rouges intenses sur la photo ci-dessus. si par contre la valeur de la phase est telle que le cosinus vaut -1, alors nous aurons une intensité multipliée par 0, car 1+ (-1) = 0. Si l'intensité est nulle, on ne voit rien, c'est l'obscurité, ce qui correspond aux ronds noirs. Alternativement, nous allons donc avoir des zones très lumineuses, et des zones très sombres.
  Dans le cas d'une zone très lumineuse, on va alors parler d'interférences lumineuses constructives, et dans le cas des zones sombres, d'interférences lumineuses destructives. Ce phénomène ne peut que s'expliquer par l'optique physique et le modèle ondulatoire de la lumière. Ces phénomènes ne peuvent par exemple pas être expliqués avec les lois de l'optique géométrique. Nous avons maintenant la réponse à la question : pourquoi dans certains cas, nous avons "lumière+lumière=lumière", dans d'autres "lumière+lumière=obscurité".
  Voilà, on en a fini avec la partie théorique, mais qui était nécessaire pour comprendre les interférences constructives et desctructives, car elles sont utilisées dans les lecteurs de CD et de DVD.