MacBidouille

Le modèle ondulatoire de la lumière

  Cette première page va être plutôt théorique, avec des notions de physique sur les ondes. Scientifiquement parlant, on appelle onde une grandeur physique dépendant de l'espace et du temps, solution d'une équation aux dérivées partielles où les variables d'espace et de temps interviennent.
  Cela ne veut sûrement rien dire pour une grande partie d'entre vous, on va donc traduire cette définition en français :-)
  Imaginons une source lumineuse quelconque, par exemple une bougie. Si vous êtes juste à côté, vous voyez très bien la lumière. Par contre, plus vous vous éloignez, moins vous voyez la lumière produite par la bougie. L'onde lumineuse créée par la bougie n'est pas en mesure d'éclairer tout l'univers ; au delà d'une certaine distance, l'onde lumineuse créée par la bougie n'apporte plus rien. On se rend ainsi bien compte que d'une certaine manière, l'onde lumineuse dépend de la distance. L'onde lumineuse dépend de la variable que l'on appelle variable d'espace, et que l'on va noter x.
  L'onde lumineuse (ou tout autre type d'onde d'ailleurs) dépend de la variable d'espace, mais aussi de la variable temporelle, que l'on va noter t. En effet, une onde possède une certaine vitesse de propagation, qui n'est pas infinie. Certes, cette vitesse est très grande dans le cas de la lumière, mais elle est déjà beaucoup plus faible pour une onde sonore. C'est ce que l'on constate avec les éclairs par exemple : l'onde lumineuse se propage très rapidement, ce qui fait que vous voyez l'éclair quasi immédiatement. Par contre, l'onde sonore se propage bien plus lentement, vous "entendez" donc l'éclair après l'avoir vu. En mesurant le temps qui s'écoule entre le moment où vous voyez l'éclair et le moment où vous l'entendez, on peut même par un petit calcul savoir à quelle distance a eu lieu l'éclair. Une onde dépend donc aussi du temps.
  En plus de dépendre des deux variables d'espace et du temps, une onde est caractérisée par son amplitude et sa phase. L'amplitude, ce n'est pas difficile à comprendre. Vous prenez deux ampoules, une de 20 Watts par exemple, et une autre de 100 Watts. Si vous allumez les deux ampoules et que vous êtes à la même distance des deux ampoules au même moment, l'une éclaire plus que l'autre a priori. Pourtant, en étant à la même distance des deux ampoules au même moment, ce ne sont donc pas les deux variables d'espace et de temps qui peuvent avoir une influence. C'est vous l'avez compris l'amplitude (ou l'intensité) de l'onde lumineuse qui joue un rôle.
  La phase d'une onde est une autre notion qui est un peu plus délicate à comprendre, je ne vais donc pas trop m'étendre dessus, juste le strict nécessaire à la compréhension de la suite de l'article. Basons nous sur un petit exemple : on reprend notre bougie, et on la place à côté d'un miroir. La bougie va éclairer dans toutes les directions. De la lumière va aller directement vers votre oeil, une autre partie de la lumière va aller sur le miroir et se réfléchir ensuite, et aller jusqu'à votre oeil. Dans les deux cas, on va dire que les ondes lumineuses sont identiques (elles viennent d'une même bougie qui éclaire uniformément dans toutes les directions, donc pas de raison que l'onde 1 qui va vers votre oeil ne soit pas la même que l'onde 2 qui va d'abord sur le miroir avant de se réfléchir). Nous avons donc deux ondes identiques, mais qui n'ont pas pris le même chemin pour venir à votre oeil. Comme la vitesse de propagation de l'onde, même si elle est très rapide, n'est pas infinie, les ondes lumineuses 1 et 2 qui sont pourtant parties en même temps de la bougie ne vont pas arriver en même temps à votre oeil. L'oeil humain ne le voit pas, car il n'est sensible qu'à l'intensité lumineuse (l'amplitude de l'onde lumineuse), mais pas à la phase de l'onde. Pourtant, même si l'oeil ne le voit pas, il y a bien un décalage temporel entre les deux ondes qui arrivent à votre oeil. Ce décalage se mesure en faisant la différence entre la phase de chacune des ondes. L'onde 1 a une phase 1, l'onde 2 a une phase 2. Ce que l'on appelle le déphasage correspond à la différence entre la phase 1 et la phase 2. La notion de phase n'est pas facile à comprendre, mais elle est capitale pour le reste de l'article. En plus de l'amplitude, l'onde va donc être aussi caractérisée par sa phase, notée avec la lettre phi.
  Mathématiquement, on va donc retenir ceci : une onde dépend de deux grandeurs, l'espace et le temps, qui seront représentées par la variable d'espace x et la variable du temps t. De plus une onde est caractérisée par son amplitude (son intensité), que l'on va noter A, et sa phase que l'on va noter par la lettre grecque phi :

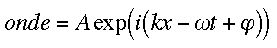
  Ceci représente l'écriture sous forme complexe de l'équation d'une onde. On y retrouve en plus de la fonction exponentielle l'amplitude A, la phase phi, et les variables de l'espace et du temps x et t. S'y rajoute un autre terme que je n'ai pas encore expliqué : oméga (le truc qui ressemble à un w). Ce terme là représente la pulsation de l'onde. Une onde sonore peut représenter un son grave ou un son aigu. Une onde lumineuse peut être rouge, verte, bleue, etc. L'intensité d'une onde ne suffit pas à expliquer ces différences. On peut avoir du rouge intense, du vert intense, du bleu intense, ... La pulsation est la grandeur qui nous manquait pour caractériser cela. Cette pulsation est reliée directement à ce que l'on appelle la longueur d'onde et qui se note avec la lettre grecque lambda.
  Reste encore la lettre k dans l'équation de l'onde. k représente la norme du vecteur d'onde, mais on n'en a pas besoin ici, donc je n'insiste pas dessus. Le petit i représente le nombre complexe imaginaire. Je n'insiste pas non plus sur ce point mathématique qui ne va pas nous être utile ici.
  Voilà donc pour cette introduction au modèle ondulatoire de la lumière. J'espère que cela n'a pas été trop dur à comprendre, car ce n'est pas facile de vulgariser tout cela. La page suivante est du même genre, car on va faire quelques calculs avec cette équation, mais ça ira mieux ensuite. Toute cette partie théorique est cependant nécessaire pour bien comprendre les phénomènes physiques mis en jeu.